PCA..?
📝 PCA (Principle Component Analysis: 주성분 분석)이란 데이터분석 관련 분야에서 "데이터의 특징을 최대한 보존하면서 차원을 낮추는 방법"으로 사용되었다.
머신러닝이나 딥러닝에서 데이터를 분석하는 것에 있어 차원이 많아질수록 복잡하고 직관적으로 데이터를 해석할 수 없다.
따라서 데이터의 특징을 최대한 유지하면서 차원을 축소하는 과정은 중요하다. 물론 자율주행 시스템의 인지관련에서도 카메라 비전쪽에서 딥러닝을 사용하거나 라이다 딥러닝을 할 경우에도 데이터 분석이 중요하기에 차원축소 용도로 PCA가 활용될 수 있다.
또한, 여러 논문에서의 내용을 바탕으로 PCA가 차원 축소 뿐만 아니라 다양한 데이터 분석에 어떻게 사용될 수 있는지도 정리하였다.
(라이다 pcd를 기하학적인 측면에서 PCA 활용할 수 있는 방안에 대한..)
📝 ***PCA :: 직관적인 해석***
[2차원 데이터 분석에 대한 PCA 적용]
이해하기 편한 유튜브 영상을 발견하여 해당 영상의 내용을 캡쳐하여 정리하도록 하겠다.
https://www.youtube.com/watch?v=FgakZw6K1QQ
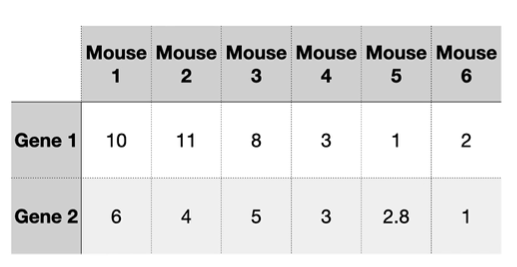
위의 그림과 같이 쥐의 유전자1과 유전자2에 대한 데이터가 존재한다고하자 이러한 2차원 데이터는 2차원 직교좌표계에 나타내면 아래 그림과 같다
여기서 데이터를 보고 알 수 있는 것은 쥐 1,2,3이 gene1과 gene2 에대해 서로 비슷하고 쥐 4,5,6이 서로 비슷하다는 것을 알 수 있다. 이렇게 2개의 항목으로 쥐의 특성을 분류한다면 너무나도 편하다. 물론 PCA도 존재하지 않았겠다.
하지만 쥐의 유전자를 예시로 들더라도 수 많은 유전자 특징에 따라 쥐의 특성을 표현할 수 있다. 따라서 데이터에 많은 차원이 존재하는 것은 당연한 얘기이다.
PCA의 적용에 대해 직관적으로 살펴보면 우선 각 항목에 대한 평균값을 구한다. 이렇게 구한 평균값은 데이터를 원점을 기준으로 나열하는 것에 활용된다.
앞서 구한 평균값을 기준으로 데이터를 원점을 기준으로 정렬하면 위의 그림과 같다.
위의 그림처럼 빨간색 점선으로 임의로 그린다. 이때 각각의 점들을 임의로 그린 선에 투영하는데 원점에서부터 각각의 데이터들을 빨간색 점선에 투영시킨 점까지의 거리를 dn(n =1,2,3,4,5,6)이라고 하였을 때 각각의 dn의 제곱의 합이 최대가 되는 선을 찾는다.
위의 그림은 dn의 제곱의 합이 최대가 되도록 하는 점선이다. 이를 주축이라 부른다.
만약에 위의 그림처럼 주축의 기울기가 1/4라고 한다면 이를 고려하여 아래 그림과 같이 주축에 대해 데이터를 나열할 때 Gene 1 값과 Gene2값이 어떤 비율로 반영되는지를 구할 수 있다.
이는 gene1을 0.97만큼, gene2를 0.242만큼 구성한 단위벡터임을 알 수 있다. 이를 우리는 singular vector 혹은 eigen vector라고 부른다.
더 나아가 dn의 제곱의 합을 SS라고 할 때 SS(PC1에 대한 거리)를 Eigenvalue라고 하고 SS의제곱근을 singular value라고 한다.
PC2의 경우 PC1에 직교하는 선을 의미한다. 따라서 PC2는 PC1과 반대로 -0.242만큼의 gene1과 0.97만큼의 gene2로 구성된다.
이를 다시 회전시키면 위의 그림과 같이 데이터가 새로운 PC1, PC2축을 기준으로 정렬하게 된다.
앞서 언급한 Eigen value 값이 PC1은 15 PC2는 3이라고 할 때 PC1의 경우 전체 데이터의 분산에 대해 83% (15/18)을 차지하고 PC2의 경우 전체 데이터의 분산에 17%를 차지한다.
[3차원 데이터 분석에 대한 PCA 적용]
3차원의 경우 어렵게 생각할 것 없다. 우선 데이터의 평균을 구하고 원점을 기준으로 정렬하도록 한다. 이후 주축을 찾는다. 앞서 언급했듯이 주축의 경우 모든 데이터 셋에 대해 원점에서부터 주축에 내린 수선의 발까지의 거리의 제곱 합이 최대가 되는 즉, SS가 최대값이 되도록 하는 선을 찾으면 된다. 만약 주축을 찾았다면 위의 그림에서 좌측에 표시된 수처럼 gene1, gene2와 gene3에 대한 비율이 주어진다. (기울기를 아니깐..) 비율값을 살펴보면 gene3가 가장 큰 영향을 주는 것임을 알 수 있다.
PC2의 경우 PC1과 직교하면서 SS가 최대가 되는 선을 찾는다. 이렇게 찾게 되면 위의 그림에서 좌측에 나온 숫자 조합으로 새롭게 정렬될 데이터 값을 구할 수 있다. 이를 살펴보면 gene1이 PC2에서 가장 많은 영향을 미치는 것을 알 수 있다.
마지막으로 PC3의 경우 PC2와 PC1에 서로 직교한다.
각각의 주축에 대해 eigen value를 구하면 각 주축이 데이터의 분산도에 얼마만큼의 비율을 차지하는지 알 수 있다. 만약 3차원 데이터를 2차원으로 표현할 때 데이터의 특징을 유지하고 싶다고 한다면 전체 데이터의 79%를 차지하는 PC1과 15%를 차지하는 PC2를 기준으로 2차원으로 데이터를 표현할 것이다,.
이처럼 3차원이상의 고차원의 데이터를 데이터의 특성을 유지하면서 저차원으로 차원축소를 하는 PCA에 대해 직관적인 측면으로 알아보았다.
📝 ***PCA: : 수학적인 해석***
PCA (Principle Component Analysis) : 주성분 분석 이란?
위의 블로그의 도움으로 수학적인 면에서 PCA를 이해할 수 있었다.
우선 “직관적인 해석” 차원에서 보았을 때 차원 축소는 전체 데이터의 분산을 많이 갖는 주축을 바탕으로 수행하였다. 여기서 중요한 것은 분산이다.
분산이란..
데이터의 분포를 표현하는 값이다. 위의 “직관적인 해석”에서 eigen value를 원점에서 부터 주축에 수선의 발까지의 거리라고 하였다. 이를 다르게 말하면 표준편차이다. SS는 표준편차의 제곱의 합이였다. 이를 n-1로 나눈 것이 분산이다.
이처럼 데이터의 분포 즉, 특징을 파악하는 것에 있어 분산이 중요한데 고차원의 경우 covariance가 존재한다
수학적으로 계산하기 위해서 covariance matrix가 활용된다.
covariance의 대각 원소의 경우 각 축에 대한 분산으로 적용된다.
만약 위의 그림의 우측 그래프처럼 데이터가 정렬되었고 이의 covariance를 구하면 그림의 좌측과 같다고 할 때 해석할 수 있는 것은 x축에 대해 데이터의 분산이 크다는 것을 알 수 있다. 반면에 y축에 대해서는 분산이 작은것을 알 수 있다.
반면에 covariance matrix를 기준으로 선형변환을 하여 데이터를 표현할 수도 있다. 위의 그림의 좌측 그래프에서 원점을 기준으로 고르게 퍼져있는 normal distributed 데이터를 covariance matrix 원소값을 통해 선형 변환하여 원래 데이터의 분포를 표현할 수 있다.
이는 아래의 그림과 같이 eigen value eigen vector로 표현 가능하다고 말할 수 있다.
위의 그림에서 선형 변환을 하더라도 방향이 변하지 않는 vector가 존재한다. 이를 Eigen vector라고 한다.
PCA를 수행하는 수학적인 절차는 아래와 같이 정리할 수 있다.
- 고차원의 data set에 대한 covariance matrix를 구한다.
- 구한 covariance matrix에 대하여 Eigen value와 Eigen vector를 구한다.
- 구한 Eigen value가 작은 순으로 정렬한다.
- 차원 축소시 원하는 비율의 Eigen vector를 사용하여 차원을 축소한다.
📝 ***PCA: : 다양한 활용***
PCA를 차원 축소의 측면에서 뿐만 아니라 다양한 측면에서 사용 가능하다. 최근에 정리한 여러 논문을 바탕으로 다양한 PCA를 활용하는 것을 살펴볼 수 있었는데 이를 정리해 보겠다.
- *[Ground Segmentation] (Patchwork: Concentric Zone-based Region-wise Ground Segmentation with Ground Likelihood Estimation Using a 3D LiDAR Sensor Hyungtae Lim1, Student Member, IEEE, Minho Oh1, Hyun Myung1, Senior Member, IEEE)*
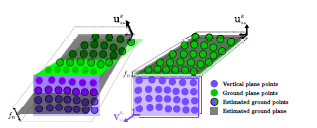
논문에 실려있는 그림을 인용하겠다. 지면 인식을 위해 어느 한 영역(bin) 안에 있는 pcd들의 covariance matrix (\*\*c ∈ R$^3$\*\*)를 구하고 egien value를 크기 순으로 나열하면 가장 작은 eigen value값을 갖는 경우 eigen vector를 지면의 법선벡터로 여긴다. 이 이유는 지면이 어느정도 평평하다고 가정하였을 때 데이터의 분산이 가장 작은 것이 당연하다. (위의 그림은 정확하게 연석의 수직한 부분을 찾는 과정으로 연석의 벽면에 해당하는 pcd의 covariance matrix를 통해 eigen value를 구하였을 때 eigen value가 가장 작은 eigen vector가 연석의 수직한 부분에 대한 법선 벡터이다.)이는 PCA를 차원 축소의 방법이 아니라 데이터의 특성을 파악하는 방안으로 사용된 예시이다. - [Global Place Recognition] (Global Place Recognition using An Improved Scan Context for LIDAR-based Localization System Xiaoyu Shi, Ziqi Chai, Yan Zhou, Jianhua Wu Member, IEEE and Zhenhua Xiong Member, IEEE)
Scan Context는 Lidar scene을 polar coordinate를 기준으로 bin을 나누어 각각의 bin만다 최대 z값을 matrix의 원소로하는 global descriptor이다. Global Place Recognition을 할 때 Scan Context를 활용하는데 Scan Context는 Lidar의 정면 방향을 0도로 함을 기준으로 colunm값을 정렬한다. 따라서 같은 장소라도 다른 방향에서 본 Scan Context 끼리 cosine 유사도를 측정하면 상이한 결과가 나올 수 있다._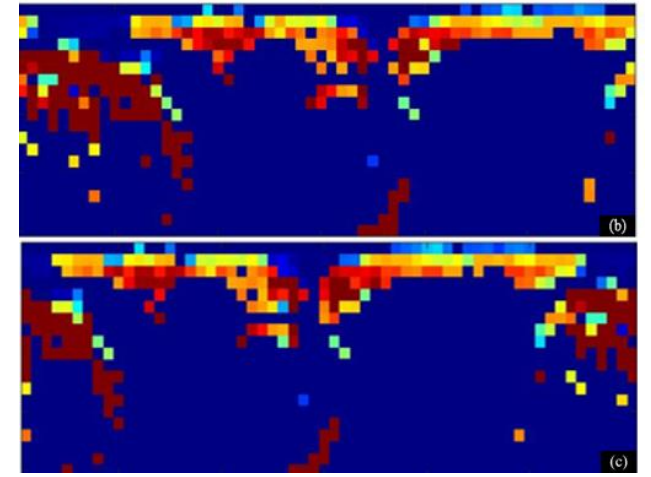
(b)와 (c)는 같은 장소의 LiDAR scene을 서로 다른 방향으로 보았을 때 만든 Scan Context이다. column방향으로 shift가 발생했음을 알 수 있다.하지만 위의 논문에서 제시한 방법은 PCD의 Scan Conext를 Lidar의 정면 방향을 기준으로 나열하는 것이나 아니라 PCD의 PCA를 적용해 point들의 분포를 기준으로 주축을 만들어 주축의 방향으로 (eigen value가 가장 큰 eigen vector의 방향) column을 설정해 연산량을 줄임과 동시에 더 정보를 보존하여 좀 더 정확한 global place recognition을 수행하였다.
사진 (a)는 pcd에 PCA를 적용하여 주축을 구하는 과정이다. 이때 z축은 고정하고 x와 y축에 대해서만 PCA를 적용하는데 그 이유는 Scan Context가 bin 영역 내의 최대 z값을 matrix의 원소로 하기 때문에 이를 보존하는 것이다. 이는 논문에서 PCA를 차원 축소의 용도가 아니라 data 특성을 알아내는 용도로 사용한 것이다. 마지막 단계를 보면 바라보는 방향이 달랐는데 Scan Context를 만들 때에는 특정 방향으로 축이 설정됨을 볼 수 있다.